I'll assume the usual definition of set difference,
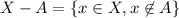 .
.
Let
 . Then
. Then
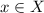 and
and
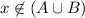 . If
. If
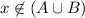 , then
, then
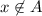 and
and
 . This means
. This means
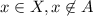 and
and
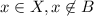 , so it follows that
, so it follows that
 . Hence
. Hence
 .
.
Now let
 . Then
. Then
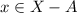 and
and
 . By definition of set difference,
. By definition of set difference,
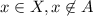 and
and
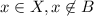 . Since
. Since
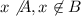 , we have
, we have
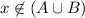 , and so
, and so
 . Hence
. Hence
 .
.
The two sets are subsets of one another, so they must be equal.
The proof of this is the same as above, you just have to indicate that membership, of lack thereof, holds for all indices
 .
.
Proof of one direction for example:
Let
 . Then
. Then
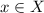 and
and
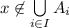 , which in turn means
, which in turn means
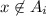 for all
for all
 . This means
. This means
 , and
, and
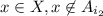 , and so on, where
, and so on, where
 , for all
, for all
 . This means
. This means
 , and
, and
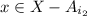 , and so on, so
, and so on, so
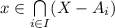 . Hence
. Hence
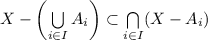 .
.