Question

Prove that if n is a perfect square, then n+1 can never be a perfect square

Answer 1

Proved

Explanation:

To prove that if n is a perfect square, then n+1 can never be a perfect square

Let n be a perfect square

`n=x^2`

Let
`n+1 = y^2`

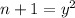
Subtract to get

`1 = y^2-x^2 =(y+x)(y-x)`

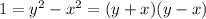
Solution is y+x=y-x=1

This gives x=0

So only 0 and 1 are consecutive integers which are perfect squares

No other integer satisfies y+x=y-x=1