Question

Calculate capacitance of two parallel flat circular conducting plates with a space d between them and radius R>>d. How good an approximation is your result?

Answer 1

`C=\epsilon_(o)(\pi R^_(2))/(d)`

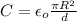
This result is a very good approximation, because R>>d

Step-by-step explanation:

The capacitance for two parallel flat plates, with surface S, space between them d, is:

`C=\epsilon_(o)(S)/(d) =\epsilon_(o)(\pi R^_(2))/(d)`

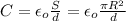
This calculation is based on the fact that the electric field is constant between the plates. This only happens if the area of the plates is much larger than the distance between them: S>>d, i.e. R>>d. If we assume these factors, the result has a very good approximation.