Question

A disk with radius of 0.4 m is rotating about a centrally located axis with an angular acceleration of 0.3 times the angular position theta. The disk starts with an angular velocity of 1 rad/s when theta = 0. Determine the magnitudes of the normal and tangential components of acceleration of a point P on the rim of the disk when theta has completed one revolution.

Answer 1

a₁= 1.98 m/s² : magnitud of the normal acceleration

a₂=0.75 m/s² : magnitud of the tangential acceleration

Step-by-step explanation:

Formulas for uniformly accelerated circular motion

a₁=ω²*r : normal acceleration Formula (1)

a₂=α*r: normal acceleration Formula (2)

ωf²=ω₀²+2*α*θ Formula (3)

ω : angular velocity

α : angular acceleration

r : radius

ωf= final angular velocity

ω₀ : initial angular velocity

θ : angular position theta

r : radius

Data

r =0.4 m

ω₀= 1 rad/s

α=0.3 *θ , θ= 2π

α=0.3 *2π= 0,6π rad/s²

Magnitudes of the normal and tangential components of acceleration of a point P on the rim of the disk when theta has completed one revolution.

We calculate ωf with formula 3:

ωf²= 1² + 2*0.6π*2π =1+2.4π ²= 24.687

ωf=
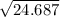`√(24.687)` =4.97 rad/s

a₁=ω²*r = 4.97²*0.4 = 1.98 m/s²

a₂=α*r = 0,6π * 0.4 = 0.75 m/s²