Answer:
a) must be met
Explanation:
We have two conditions:
a) For every
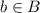 and
and
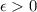 , there exists
, there exists
 , such that
, such that
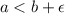 .
.
b) There exists
 and
and
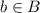 such that
such that
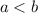 .
.
We will prove that conditon a) is equivalent to

If a) is not satisfied, then it would exist
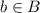 and
and
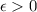 such that, for every
such that, for every
 ,
,
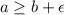 . This implies that
. This implies that
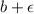 is a lower bound for A and in consequence
is a lower bound for A and in consequence
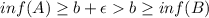
Then,
 implies a).
implies a).
If
 is not satisfied then,
is not satisfied then,
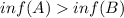 and in consequence exists
and in consequence exists
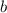 such that
such that
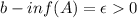 . Then
. Then
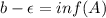 and, for every
and, for every
 ,
,
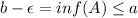 .
.
So, a) is not satisfied.
In conclusion, a) is equivalent to

Finally, observe that condition b) is not an appropiate condition to determine if
 or not. For example:
or not. For example:
- A={0}, B={1}. b) is satisfied and
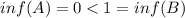
- A={0}. B={-1,1}. b) is satisfied and
