Answer: -2.12°C
Explanation:
Let x denotes the reading of the thermometers .
We assume that the readings on the thermometers are normally distributed.
Let a be the reading that separates the rejected thermometers from the others.
Given: Population mean :
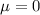
Standard deviation:

Also,

By using the z-table , the z-value corresponds to the p-value (one -tailed)0.017 is
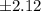 .
.
Now,
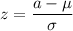
i.e.
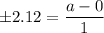
i.e.
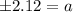
For left tailed ,
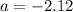
It means the reading that separates the rejected thermometers from the others = -2.12°C.