Question

A swan on a lake becomes airborne by flapping its wings and running on top of the water. If the swan must reach a velocity of 6.50 m/s to take off and it accelerates from rest at an average rate of 0.350 m/s2 , what distance Δx does it travel before becoming airborne?

Answer 1

The distance traveled by the swan is 60.35 meters.

Step-by-step explanation:

Given that,

A swan accelerate from rest (u = 0) to 6.5 m/s to take off.

Acceleration of the swan,
`a=0.35\ m/s^2`

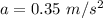
We need to find the distance Δx it travel before becoming airborne. From the third equation of motion as :

`\Delta x=(v^2-u^2)/(2a)`

`\Delta x=((6.5)^2)/(2* 0.35)`

`\Delta x=60.35\ m`

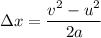
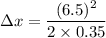
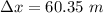
So, the distance traveled by the swan is 60.35 meters. Hence, this is the required solution.