Question

If y(x, t) = (4.7 mm)sin(kx + (675 rad/s)t + ϕ) describes a wave traveling along a string, how much time does any given point on the string take to move between displacements y = +2.0 mm and y = −2.0 mm?

Answer 1

It takes 0.00127 seconds.

Step-by-step explanation:

The equation its

`y(x,t) = 4.7 \ mm  \ sin ( kx + 675 (rad)/(s) t + \phi)`.

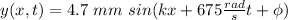We want the time for ANY POINT, so, for convenience, lets take x=0

`y(0,t) = 4.7 \ mm  \ sin ( k*0 + 675 (rad)/(s) t + \phi)`.

`y(0,t) = 4.7 \ mm  \ sin ( 675 (rad)/(s) t + \phi)`.

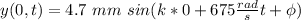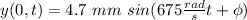Now, we want the positions

`y(0,t_1)=2 \ mm`

`y(0,t_2)=-2 \ mm`

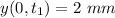
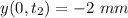
so, for the first position:

`y(0,t_1)=2 \ mm`

`2 \ mm = 4.7 \ mm  \ sin ( 675 (rad)/(s) t_1 + \phi)`.

`\frac{2 \ mm} {4.7 \ mm }=  sin ( 675 (rad)/(s) t_1 + \phi)`.

`0.42 =  sin ( 675 (rad)/(s) t_1 + \phi)`.

`sin^-1(0.42) =  675 (rad)/(s) t_1 + \phi)`.

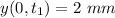
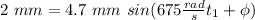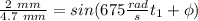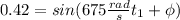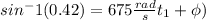and for the second one:

`y(0,t_2)=-2 \ mm`

`-2 \ mm = 4.7 \ mm  \ sin ( 675 (rad)/(s) t_2 + \phi)`.

`\frac{-2 \ mm} {4.7 \ mm }=  sin ( 675 (rad)/(s) t_2 + \phi)`.

`-0.42 =  sin ( 675 (rad)/(s) t_2 + \phi)`.

`sin^-1(0.42) =  675 (rad)/(s) t_2 + \phi)`.

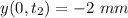
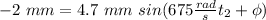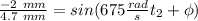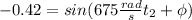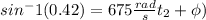Now, we can subtract both:

`sin^-1(0.42) -sin^-1(-0.42) =  675 (rad)/(s) t_1 + \phi - 675 (rad)/(s) t_2 + \phi`

`sin^-1(0.42) -sin^-1(-0.42) =  675 (rad)/(s) t_1 - 675 (rad)/(s) t_2`

`sin^-1(0.42) -sin^-1(-0.42) =  675 (rad)/(s) (t_1 - t_2)`

`(sin^-1(0.42) -sin^-1(-0.42))/( 675 (rad)/(s)) = (t_1 - t_2)`

`(0.43 - (-0.43))/( 675 (rad)/(s)) = (t_1 - t_2)`

`(0.86)/( 675 (rad)/(s)) = (t_1 - t_2)`

`0.00127 s = (t_1 - t_2)`

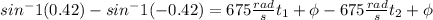
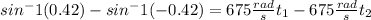
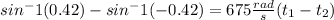
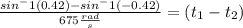
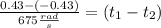
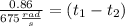
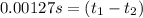
The strings take 0.00127 seconds.