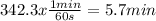Answer:
The answer is 5.7 minutes
Step-by-step explanation:
A first-order reaction follow the law of
![Ln [A] = -k.t + Ln [A]_(0)](https://img.qammunity.org/2020/formulas/chemistry/high-school/b4qlnkdz5z0nhm4wmo9fk52a2zoc4d0qwo.png) . Where [A] is the concentration of the reactant at any t time of the reaction,
. Where [A] is the concentration of the reactant at any t time of the reaction,
![[A]_(0)](https://img.qammunity.org/2020/formulas/chemistry/college/qqxha3gkqyi6nvxca57jmthzzzu8zyjq3q.png) is the concentration of the reactant at the beginning of the reaction and k is the rate constant.
is the concentration of the reactant at the beginning of the reaction and k is the rate constant.
Dropping the concentration of the reactant to 6.25% means the concentration of A at the end of the reaction has to be
![[A]=(6.25)/(100).[A]_(0)](https://img.qammunity.org/2020/formulas/chemistry/high-school/pjzj4ov3ioxzllf94kahhbiqwyyegw042q.png) . And the rate constant (k) is 8.10×10−3 s−1
. And the rate constant (k) is 8.10×10−3 s−1
Replacing the equation of the law:
![Ln (6.25)/(100).[A]_(0) = -8.10x10^(-3)s^(-1).t + Ln[A]_(0)](https://img.qammunity.org/2020/formulas/chemistry/high-school/eiwx9e3619yen5t5jda1qaol3gt7kf224n.png)
Clearing the equation:
![Ln [A]_(0).(6.25)/(100) - Ln [A]_(0) = -8.10x10^(-3)s^(-1).t](https://img.qammunity.org/2020/formulas/chemistry/high-school/105z9v46cwq8n2a04aou0orxhpe50pxw0r.png)
Considering the property of logarithms:
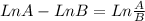
Using the property:
![Ln ([A]_(0))/([A]_(0)).(6.25)/(100) = -8.10x10^(-3)s^(-1).t](https://img.qammunity.org/2020/formulas/chemistry/high-school/qureud2to9dfr0re399xswg6jqzhdyepgi.png)
Clearing t and solving:

The answer is in the unit of seconds, but every minute contains 60 seconds, converting the units: