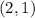Question

The coordinates of three of the vertices of parallelogram ABCD are A(1, 0), B(2, 3), C(3, 2). What are coordinates of the fourth vertex and the point of intersection of the diagonals?

Answer 1

A) The coordinates of the fourth vertex are:

1) x-coordinate:

`x=2`

2) y-coordinate:

`y=-1`

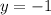
B) The point of intersection of the diagonals is:
`(2,1)`

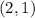
Explanation:

We need to remember that the diagonals of a parallelogram intersect each other at a half-way point and the midpoint of each diagonal is the same.

The midpoint formula is:

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

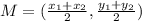
Since:

`M_(AC)=M_(BD)`

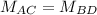
We can find the coordinates of the fourth vertex
`D(x,y)` through these procedure:

1) x-coordinate:

`(1+3)/(2)=(2+x)/(2)\\\\2(2)=x\\\\4-2=x\\\\x=2`

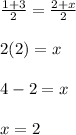
2) y-coordinate:

`(0+2)/(2)=(3+y)/(2)\\\\1(2)-3=y\\\\y=-1`

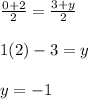
Therefore, fourth vertex is
`D(2,-1)`

Since the point of intersection of the diagonals is the midpoint of a diagonal (Remember that
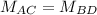`M_(AC)=M_(BD)`), this is:

`M_(AC)=M_(BD)=((1+3)/(2),(0+2)/(2))\\\\M_(AC)=M_(BD)=(2,1)`

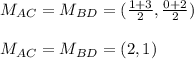
Therefore, the point of intersection of the diagonals is
`(2,1)`