Answer:
The maximum power density in the reactor is 37.562 KW/L.
Step-by-step explanation:
Given that,
Height = 10 ft = 3.048 m
Diameter = 10 ft = 3.048 m
Flux = 1.5
Power = 835 MW
We need to calculate the volume of cylinder
Using formula of volume
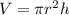
Put the value into the formula


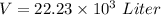
We need to calculate the maximum power density in the reactor
Using formula of power density
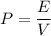
Where, P = power density
E = energy
V = volume
Put the value into the formula
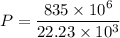
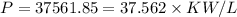
Hence, The maximum power density in the reactor is 37.562 KW/L.