Answer:
Option B.
Explanation:
It is given that ΔEFI is dilated by a scale factor of one half with the center of dilation at point F. Then, it is reflected over line a to create ΔHFG.
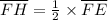
Multiply both sides by 2.
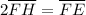
Similarly,

Multiply both sides by 2.
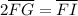
And,
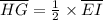
Multiply both sides by 2.
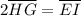
By SSS property of similarity,
ΔEFI ~ ΔGFH
Since,
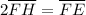 ,
,
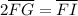 ,
,
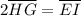 , therefore ΔEFI ~ ΔGFH.
, therefore ΔEFI ~ ΔGFH.
Therefore, the correct option is B.