Question

In the figure, side AB is given by the expression (5x + 5)/(x + 3), and side BC is (3x + 9)/(2x - 4).

The simplified expression for the area of rectangle ABCD is _______, and the restriction on x is ____.

Answer 1

The simplified expression for the area of rectangle ABCD is
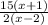`( 15(x + 1))/(2(x - 2))`, and the restriction on x is x≠2 .

Explanation:

Side AB = Width of rectangle = (5x + 5)/(x + 3)

Side BC = Length of rectangle = (3x + 9)/(2x - 4)

Area of Rectangle = Length * Width

Putting values:

`Area\,\,of\,\,rectangle =( (3x + 9))/((2x - 4)) * ((5x + 5))/((x + 3))`

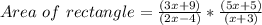
Solving,

`Area\,\,of\,\,rectangle =( 3(x + 3))/((2x - 4)) * (5x + 5)/((x + 3)) \\Area\,\,of\,\,rectangle =( 3)/(2(x - 2)) * 5x + 5\\Area\,\,of\,\,rectangle =( 3(5x + 5))/(2x - 4)\\Area\,\,of\,\,rectangle =( 15x + 15)/(2x - 4)\\Area\,\,of\,\,rectangle =( 15(x + 1))/(2(x - 2))`

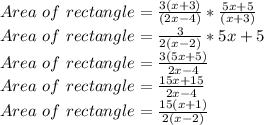
The restriction on x is that x ≠ 2, because if x =2 then denominator will be zero.

So, the answer is:

The simplified expression for the area of rectangle ABCD is
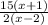`( 15(x + 1))/(2(x - 2))`, and the restriction on x is x≠2 .