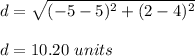Question

What is the length of the diagonal in the trapezoid below? Round to the nearest hundredth.

Answer 1

Answer:
`10.20\ units`

Explanation:

Since the given trapezoid is isosceles, its diagonals are congruent.

Observe one of the diagonals in the figure attached. To find its length we need to use formula for calculate the distance between two points:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

In this case, knowing that the endpoints of the diagonal are B(5,4) and D(-5,2), we just need to substitute values into the formula.

Then, the length of the diagonal in the trapezoid is (Rounded to the nearest hundred):

`d=√((-5-5)^2+(2-4)^2)\\\\d=10.20\ units`