Question

Which of the following is NOT equivalent to the nxn matrix A being invertible? A. The homogeneous system associated to A has a unique solution. B. Some non-homogeneous system whose coefficient matrix is A has a unique solution. C. Every non-homogeneous system whose coefficient matrix is A is consistent. D. The column space of A is R". E. The linear transformation x H Ax is one-to-one.

Answer 1

Option C

Explanation:

• For the matrix A of order
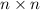  `n* n` to be invertible, its determinant must not be equal to zero, |A|
  `\\eq`0,
  `A^(- 1)` exists if- AC = CA = I, where I is identity matrix.

1. The homogeneous equation with coefficient matrix A has a unique solution:

AB = 0, B =
`A^(- 1).0 = 0`

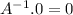
Thus, B = (0, 0, 0......., 0) is a unique solution

2. The non - homogeneous equation system with coefficient matrix A has a unique solution:

For an equation- AY = D

Y =
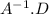`A^(- 1).D` is a unique solution

3. Every non homogeneous equation with coefficient matrix A is not consistent as:

For an equation- AY = D, has a solution.l Thus coefficient matrix is inconsistent whereas augmented matrix is.

4. Rank of matrix A = n, Thus the column space of A is
`R^(n)`

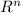
5. Since, column space of A =
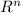`R^(n)`, thus x→xA is one-to-one