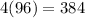Question

A rectangle is constructed with its base on the​ x-axis and two of its vertices on the parabola y equals = 100 100 minus −x squared 2. What are the dimensions of the rectangle with the maximum​ area? What is that​ area?

Answer 1

Explanation:

Given that a rectangle is constructed with its base on the x axis and two of its vertices on the parabola

`y=100-x^2`

This parabola has vertex at (0,100) and symmetrical about y axis.

Any general point above x axis can be written as (a,b) (-a,b) since symmetrical about yaxis.

Hence coordinates of any rectangle are

`(a,0) (-a,0), (a, 100-a^2), (-a, 100-a^2)`

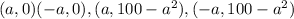
Length of rectangle = 2a and width =
`100-a^2`

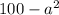
Area of rectangle = lw =
`2a(100-a^2)=200a-400a^3`

To find max area, use derivative test.

`A' = 200-800a^2\\A`

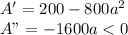
Hence maxima when first derivative =0

i.e. when a =2

Thus we find dimensions of the rectangle are l =4 and w = 96

Maximum area =
`4(96) = 384`