Question

The average life of light bulbs produced by SABA Electric Co. is believed to be normally distributed with the mean service life of 950 hours and a standard deviation of 100 hours. A random sample of 100 bulbs is tested and it has a mean life of 930 hours. Can it be concluded that the mean service life of the bulbs is less than the expectation at significant level of 0.01?

Answer 1

We cannot conclude that the mean life of the bulbs is less than 950h.

Explanation:

Be,

Sample mean (MX) = 930h

Population standard deviation (sigma) = 100h

Sample size (n) = 100

Significance level (alpha) = 0.01

Null hypothesis (H0): Mu = 950

Alternative hypothesis (Ha): Mu <950

Population mean in the null hypothesis (Mu0) = 950

Critical value (Z-alpha) = -2.32635.

The test statistic in this case is given by:

`Z_(c) = \frac{(MX - Mu0)}{\sqrt{(sigma^(2))/(n) } } = -2.000`

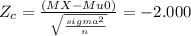
Since
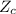`Z_(c)` is greater than Z-alpha, it is decided not to reject H0. That is, we cannot conclude that the average life of the bulbs is less than 950h.