Answer:
The area enclosed by given curves is
 square units.
square units.
Explanation:
The given equations are
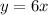
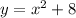
Draw the graph of given equations.
From the below graph it is clear that both curves intersect each other at (2,12) and (4,24).
The area of region enclosed by curves is
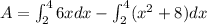
![A=6((1)/(2)[x^2]_(2)^(4))-(1)/(3)[x^3]_(2)^(4)-8[x]_(2)^(4)](https://img.qammunity.org/2020/formulas/mathematics/college/guklxxdr92uafeiqao0kx3cjgljmat63nm.png)
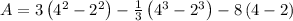
![A=3[12]-(1)/(3)[56]-8[2]](https://img.qammunity.org/2020/formulas/mathematics/college/8elrbaas7yt2acbrwji5fa47jwvw4l97iq.png)
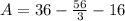
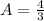
Therefore the area enclosed by given curves is
 square units.
square units.