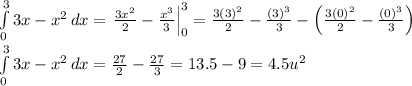Question

Sketch the region enclosed by y=3x and y=x^2 . Then find the area of the region.

How to get this answer?

Answer 1

`A=4.5u^2`

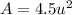
Explanation:

The integral of a function gives you the area under the curve, the subtraction of one of the areas from the other will give you the area in between.

The limits of integration are the points where the curves intersect each other(take the curves has a system of equation and solve for x and y):

`y=3x, y=x^2\\3x=x^2\\x^2-3x=0\\x(x-3)=0\\x_1=0\\x-3=0\\x_2=3`

`y_1=3x_1=3(0)=0\\y_2=3x_2=3(3)=9`

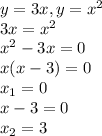
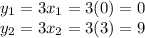
The integral will be the subtraction of the curve
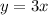`y=3x` and
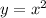`y=x^2` (In the graph you can see y=3x is the upper curve):

`\int\limits^3_0 {3x-x^2} \, dx =\left(3x^2)/(2)-(x^3)/(3)\right|^3_0=(3(3)^2)/(2)-((3)^3)/(3)-\left((3(0)^2)/(2)-((0)^3)/(3)\right)\\\int\limits^3_0 {3x-x^2} \, dx =(27)/(2)-(27)/(3) =13.5-9=4.5u^2`