Answer:
Prove by contradiction
Explanation:
If
 is even then
is even then
 is even
is even
Prove by contradiction
 is even then
is even then
 is odd
is odd
Also

Since
 is odd
is odd
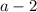 is also an odd number, the addition or subtraction of an even number with an odd number is an odd number.
is also an odd number, the addition or subtraction of an even number with an odd number is an odd number.
The multiplication of two odd numbers yields to another odd number, then
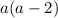 is odd but is equal to
is odd but is equal to
 which is even, a number cannot be odd and even, this is a contradiction so
which is even, a number cannot be odd and even, this is a contradiction so
 must be even.
must be even.