Question

In a Young's double-slit experiment, 610-nm-wavelength light is sent through the slits. The intensity at an angle of 2.95° from the central bright fringe is 85% of the maximum intensity on the screen. What is the spacing between the slits?

Answer 1

spacing between the slits is 405.32043 ×
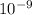`10^(-9)` m

Step-by-step explanation:

Given data

wavelength = 610 nm

angle = 2.95°

central bright fringe = 85%

to find out

spacing between the slits

solution

we know that spacing between slit is

I = 4
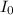`I_(0)` × cos²∅/2

so

I/4
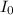`I_(0)` = cos²∅/2

here I/4
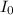`I_(0)` is 85 % = 0.85

so

0.85 = cos²∅/2

cos∅/2 = √0.85

∅ = 2 ×
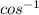`cos^(-1)` 0.921954

∅ = 45.56°

∅ = 45.56° ×π/180 = 0.7949 rad

and we know that here

∅ = 2π d sinθ / wavelength

so

d = ∅× wavelength / ( 2π sinθ )

put all value

d = 0.795 × 610×
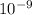`10^(-9)` / ( 2π sin2.95 )

d = 405.32043 ×
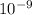`10^(-9)` m

spacing between the slits is 405.32043 ×
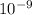`10^(-9)` m