Question

What is the equation of the circle with center (0, 0) that passes through the point (–4, –6)?

Answer 1

Option 4: x^2+y^2 = 52

Explanation:

Given

Centre at origin

Point on circle = (-4, -6)

The distance between origin and point on circle will be the radius of the circle

So,

`r = \sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)}\\r= √((-4-0)^2+(-6-0)^2) \\r = √((-4)^2+(-6)^2)\\r = √(16+36) \\r = √(52)`

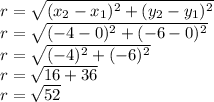
As the center is at origin the standard equation will be:

`x^2+y^2 = r^2\\`

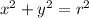
Putting the value of r

`x^2+y^2 = (√(52))^2\\x^2+y^2 = 52`

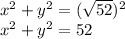
Hence, last option i.e. Option 4 is correct ..