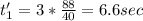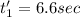Answer:
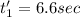
Step-by-step explanation:
the half life of the given circuit is given by
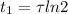
where [/tex]\tau = RC[/tex]

Given
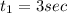
resistance in the circuit is 40 ohm and to extend the half cycle we added new resister of 48 ohm. the net resitance is 40+48 = 88 ohms
now the new half life is
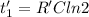
Divide equation 2 by 1
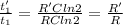

putting all value we get new half life