Given:
In
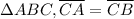 .
.
 is an altitude drawn from C to
is an altitude drawn from C to
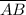 .
.
To prove:
 bisects
bisects
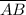 .
.
Proof:
In
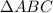 ,
,
 is an altitude drawn from C to
is an altitude drawn from C to
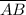 .
.
It means,
 are right angle triangles.
are right angle triangles.
In
 ,
,
Hypotenuse :
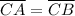 [Given]
[Given]
Leg :
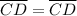 [Common]
[Common]
If the hypotenuse and leg of one right triangle are congruent to the hypotenuse and leg of another right triangle, then by HL postulate both triangles are congruent.
 [HL postulate]
[HL postulate]
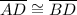 [CPCTC]
[CPCTC]
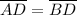
It means, point D is the midpoint of
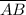 .
.
So,
 bisects
bisects
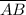 .
.
Hence proved.