Answer:
Efficiency = 52%
Step-by-step explanation:
Given:
First stage
heat absorbed, Q₁ at temperature T₁ = 500 K
Heat released, Q₂ at temperature T₂ = 430 K
and the work done is W₁
Second stage
Heat released, Q₂ at temperature T₂ = 430 K
Heat released, Q₃ at temperature T₃ = 240 K
and the work done is W₂
Total work done, W = W₁ + W₂
Now,
The efficiency is given as:

or
Work done = change in heat
thus,
W₁ = Q₁ - Q₂
W₂ = Q₂ - Q₃
Thus,
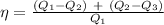
or
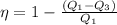
or
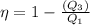
also,
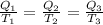
or
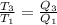
thus,
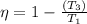
thus,
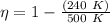
or

or
Efficiency = 52%