Answer:
The velocity of the bag will be 16.08 m/s
Step-by-step explanation:
Given:
Mass of the astronaut, M = 124 kg
Mass of the bag, m = 10 lg
Initial speed of the astronaut with bag,
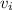 = 1.20 m/s
= 1.20 m/s
Applying the concept of conservation of momentum
we have
(M + m)
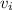 = Mv₁ + mv₂
= Mv₁ + mv₂
here,
v₁ is the final velocity of the astronaut = 0
v₂ is final velocity of the bag
thus, on substituting the values, we have
(124 + 10)1.20 = 124 × 0 + 10v₂
or
v₂ = 16.08 m/s
Hence, the velocity of the bag will be 16.08 m/s