Question

Two perpendicular lines intersect at the origin. If the slope of the first line is -1/2, what is the equation of the second line?

Answer 1

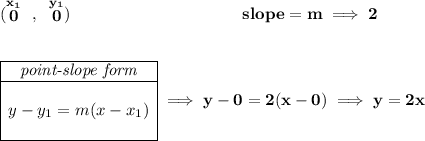
bearing in mind that perpendicular lines have negative reciprocal slopes.

now, they both intersect at 0,0, namely they both pass through it, we know the slope of the first one, so

`\bf \stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}} {\stackrel{slope}{-\cfrac{1}{2}}\qquad \qquad \qquad \stackrel{reciprocal}{-\cfrac{2}{1}}\qquad \stackrel{negative~reciprocal}{+\cfrac{2}{1}\implies 2}}`

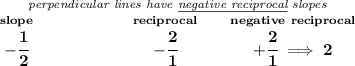
so, we're really looking for the equation of a line whose slope is 2, and runs through (0,0).

`\bf (\stackrel{x_1}{0}~,~\stackrel{y_1}{0})~\hspace{10em} slope = m\implies 2 \\\\\\ \begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-0=2(x-0)\implies y=2x`