Question

Use the construction in proof of the Chinese reminder theorem to find all solutions to the system of congruence:

x ≡ 2 ( mod 3 )

x ≡ 1 ( mod 4 )

x ≡ 3 ( mod 7 )

Answer 1

17,101,185, 269,.... is the solution.

i.e. x≡17 mod(84) is the solution

Explanation:

Given that the system is

`x ≡ 2 ( mod 3 )x ≡ 1 ( mod 4 )x ≡ 3 ( mod 7 )`

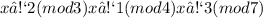
Considering from the last as 7 is big,

possible solutions would be 10,17,24,...

Since this should also be 1(mod4) we get this as 1,5,9,...17, ...

Together possible solutions would be 17, 45,73,121,....

Now consider I equation and then possible solutions are

5,8,11,14,17,20,23,26,29,...,47,....75, ....

Hence solution is 17.

Next number satisfying this would be 101, 185, ...