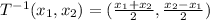Question

2. Define a linear transformation T:R^2 --> R^2 HRas follows: T(x1, x2) = (x1 - 12,21 + x2). Show that T is invertible and find T-1:

Answer 1

Answer with explanation:

T is a Linear transformation such that

`T:R^2\rightarrow R^2\\\\T(x_(1),x_(2))=(x_(1)-12,21+x_(2))`

To show that ,T is invertible that is inverse of a matrix exist ,we need to show that ,T is non singular.

⇒ |T|≠0

→→For a Homogeneous system

`(x_(1)-12,21+x_(2))=(0,0)\\\\x_(1)=12,x_(2)=-21\\\\|\text{Matrix}|=\left[\begin{array}{cc}12&0\\0&-21\end{array}\right]\\\\ |\text{Matrix}|\\eq 0`

so it is invertible.We have considered equation is of the form

`\rightarrow ax_(1)+bx_(2)+c=0`

→→For a Non Homogeneous system

`(x_(1)-12,21+x_(2))=(s,v)\\\\x_(1)=12+s,x_(2)=-21+v\\\\|\text{Matrix}|=\left[\begin{array}{cc}12+s&0\\0&v-21\end{array}\right]\\\\ |\text{Matrix}|=(s+12)* (v-21)\\eq 0`

so T, is invertible.

`T^(-1)=(Adj.T)/(|T|)\\\\T=\left[\begin{array}{cc}s+12&0\\0&v-21\end{array}\right]\\\\Adj.T=\left[\begin{array}{cc}v-21&0\\0&s+12\end{array}\right]\\\\T^(-1)=\frac{\left[\begin{array}{cc}v-21&0\\0&s+12\end{array}\right]}{(s+12)* (v-21)}\\\\T^(-1)={\left[\begin{array}{cc}(1)/(s+12)&0\\0&(1)/(v-21)\end{array}\right]}\\\\\text{Replacing s by} x_(1)\\\\ \text{and v by} x_(2), \text{we get}\\\\T^(-1)={\left[\begin{array}{cc}(1)/(x_(1)+12)&0\\0&(1)/(x_(2)-21)\end{array}\right]}`

Answer 2

`T^(-1)(x_1,x_2)=((x_1+x_2)/(2),(x_2-x_1)/(2))`

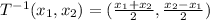
Explanation:

Given:

Linear transformation,

`T:R^2\rightarrow R^2` defined as

`T(x_1,x_2)=(x_1-x_2,x_1+x_2)`

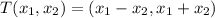
To Show: T is invertible

To find:
`T^(-1)`

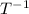
We know that Standard Basis of R² is
`\{e_1=(1,0)\:,\:e_2=(0,1)\}`

`T(e_1)=T(1,0)=(1,1)=1e_1+1e_2`

`T(e_2)=T(0,1)=(-1,1)=-1e_1+1e_2`

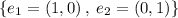
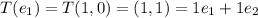
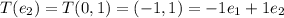
So, The matrix representation of T is
`\begin{bmatrix}1&1\\-1&1\end{bmatrix}^T=\begin{bmatrix}1&-1\\1&1\end{bmatrix}`

Now, Determinant of T = 1 - (-1) = 1 + 1 = 2 ≠ 0

⇒ Matrix Representation of T is Invertible matrix.

⇒ T is invertible Linear Transformation.

Hence Proved.

let,

`x_1-x_2=u.........................(1)`

`x_1+x_2=v.........................(2)`

Add (1) and (2),

`2x_1=u+v`

`x_1=(u+v)/(2)`

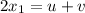
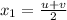
Putting this value in (1),

`(u+v)/(2)-x_2=u`

`x_2=(u+v)/(2)-u`

`x_2=(u+v-2u)/(2)`

`x_2=(v-u)/(2)`

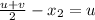
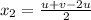
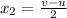
Now,

`T(x_1,x_2)=(x_1-x_2,x_1+x_2)=(u,v)`

`\implies(x_1,x_2)=T^(-1)(u,v)`

`\implies T^(-1)(u,v)=((u+v)/(2),(v-u)/(2))`

`\implies T^(-1)(x_1,x_2)=((x_1+x_2)/(2),(x_2-x_1)/(2))`

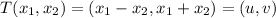
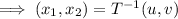
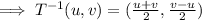
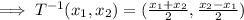
Therefore,
`T^(-1)(x_1,x_2)=((x_1+x_2)/(2),(x_2-x_1)/(2))`