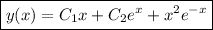Question

Observe that x and e^x are solutions to the homogeneous equation associated with:

(1-x)y'' + xy' - y = 2(x - 1)^2 e^-x

Use this fact to solve the nonhomogeneous equation.

Please explain step by step and show your work, thank you. From left to right it's y double prime .... + xy prime....

Answer 1

To take advantage of the characteristic solutions
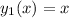`y_1(x)=x` and
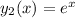`y_2(x)=e^x`, you can try the method of variation of parameters, where we look for a solution of the form

`y=y_1u_1+y_2u_2`

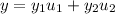
with the condition that

`{u_1}'y_1+{u_2}'y_2=0`

`\implies{u_1}'x+{u_2}'e^x=0`
`(\mathbf 1)`

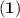
Then

`y'={y_1}'u_1+y_1{u_1}'+{y_2}'u_2+y_2{u_2}'`

`\implies y'={y_1}'u_1+{y_2}'u_2`

`y''={y_1}''u_1+{y_1}'{u_1}'+{y_2}''u_2+{y_2}'{u_2}'`

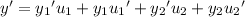
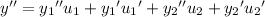
Substituting into the ODE gives

`(1-x)({y_1}''u_1+{y_1}'{u_1}'+{y_2}''u_2+{y_2}'{u_2}')+x({y_1}'u_1+{y_2}'u_2)-y_1u_1+y_2u_2=2(x-1)^2e^(-x)`

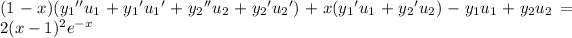
Since

`y_1=x\implies{y_1}'=1\implies{y_1}''=0`

`y_2=e^x\implies{y_2}'=e^x\implies{y_2}''=e^x`

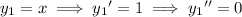
the above reduces to

`(1-x)({u_1}'+e^x{u_2}')=2(x-1)^2e^(-x)`

`{u_1}'+e^x{u_2}'=2(1-x)e^(-x)`
`(\mathbf 2)`

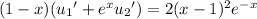
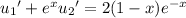
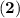
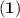`(\mathbf 1)` and
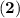`(\mathbf 2)` form a linear system that we can solve for
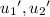`{u_1}',{u_2}'` using Cramer's rule:

`{u_1}'=(W_1(x))/(W(x)),{u_2}'=(W_2(x))/(W(x))`

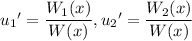
where
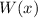`W(x)` is the Wronskian determinant of the fundamental system and
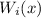`W_i(x)` is the same determinant, but with the
`i`-th column replaced with
`(0,2(x-1)^2e^(-x))`.

`W(x)=\begin{vmatrix}x&e^x\\1&e^x\end{vmatrix}=e^x(x-1)`

`W_1(x)=\begin{vmatrix}0&e^x\\2(x-1)^2e^(-x)&e^x\end{vmatrix}=-2(x-1)^2`

`W_2(x)=\begin{vmatrix}x&0\\e^x&2(x-1)^2e^(-x)\end{vmatrix}=2xe^(-x)(x-1)^2`

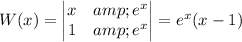
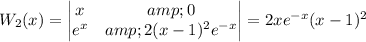
So we have

`{u_1}'=(-2(x-1)^2)/(e^x(x-1))\implies u_1=2xe^(-x)`

`{u_2}'=(2xe^(-x)(x-1)^2)/(e^x(x-1))\implies u_2=-x^2e^(-2x)`

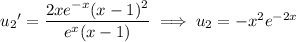
Then the particular solution is

`y_p=2x^2e^(-x)-x^2e^(-x)=x^2e^(-x)`

giving the general solution to the ODE,

`\boxed{y(x)=C_1x+C_2e^x+x^2e^(-x)}`