Proof:
Let's Multiply them!
![AB = \left[\begin{array}{ccc}1&2\\-1&4\\\end{array}\right]\left[\begin{array}{ccc}2/3&-1/3\\1/6&1/6\\\end{array}\right]=\left[\begin{array}{ccc} 1(2/3) + 2(1/6) & 1(-1/3) + 2(1/6)\\-1(2/3) + 4(1/6)&-1(-1/3) + 4(1/6)\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/ysmpon5jtuk9wxj5gmue5p5c3puyzj779f.png)
If you don't remember how to multiply matrices, don't worry. In order to get AB we focus on the rows of A, and the columns of B.
- The first row of A is [1 2] and the first column of B is [2/3 1/6], if we do de dot multiplication we get 1(2/3) + 2(1/6) = 2/3 + 1/3 = 1.
- The first row of A is [1 2] and the second column of B is [-1/3 1/6]. Here we get 1(-1/3) + 2(1/6) = -1/3 + 1/3 = 0.
- The second row of A is [-1 4] and the first column of B is [2/3 1/6]. Here we get -1(2/3) + 4(1/6) = -2/3 + 2/3 = 0.
- The second row of A is [-1 4] and the second column of B is [-1/3 1/6]. Here we get -1(-1/3) + 4(1/6) = 1/3 + 2/3 = 1.
Then
![AB = \left[\begin{array}{ccc}1&0\\0&1\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/dvkayh0m5qvun6gw92nht72gioqqz27kof.png)
We also have to see what happens with
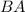 .
.
![BA = \left[\begin{array}{ccc}2/3&-1/3\\1/6&1/6\\\end{array}\right]\left[\begin{array}{ccc}1&2\\-1&4\\\end{array}\right] = \left[\begin{array}{ccc} (2/3)(1) + (-1/3)(-1) & (2/3)(2) + (-1/3)(4)\\(1/6)(1) + (1/6)(-1)&(1/6)(2) + (1/6)(4)\\\end{array}\right]= \left[\begin{array}{ccc}1&0\\0&1\\\end{array}\right]]()
With this, we can conclude that

where
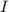 is the identity matrix. An by definition, that means that
is the identity matrix. An by definition, that means that
 and
and
 are multiplicative inverses.
are multiplicative inverses.