Question

A chemist wishing to do an experiment requiring 47Ca2+(half-life = 4.536 days) needs 5.00 g of the nuclide. What mass of 47CaCO3must be ordered if it takes 48.0 h for delivery from the supplier?

Answer 1

Answer: The answer is 6.78 grams.

Explanation: The equation used for solving this type of problems is:

`(N)/(N_0)=((1)/(2))^n`

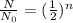
where,
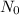`N_0` is the initial amount of radioactive substance, N is the remaining amount and n is the number of half lives.

Number of half lives is calculated on dividing the given time by the half life.

n = time/half life

Time is given as 48.0 hours and the half life is given as 4.536 days. let's make the units same and for this let's convert the half life from days to hours.

`4.536days((24hours)/(1day))`

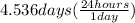
= 108.864 hours

So,
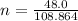`n=(48.0)/(108.864)` = 0.441

Since 5.00 g is the required amount when the radioactive substance is delivered to the scientist, it would be the final amount that is N. We need to calculate the initial amount. Let's plug in the values in the equation:

`(5.00)/(N_0)=((1)/(2))^0^.^4^4^1`

`(5.00g)/(N_0)=0.737`

`N_0=(5.00g)/(0.737)`

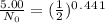
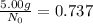
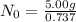
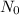`N_0` = 6.78 g

So, 6.78 g of the radioactive substance needs to be ordered.