Answer : The entropy change for the surroundings of the reaction is, -198.3 J/K
Explanation :
We have to calculate the entropy change of reaction
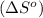 .
.
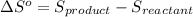
![\Delta S^o=[n_(NH_3)* \Delta S^0_((NH_3))]-[n_(N_2)* \Delta S^0_((N_2))+n_(H_2)* \Delta S^0_((H_2))]](https://img.qammunity.org/2020/formulas/chemistry/high-school/hrp43vwk8ya86e66u3vpykrfru32rd75la.png)
where,
 = entropy of reaction = ?
= entropy of reaction = ?
n = number of moles
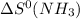 = standard entropy of
= standard entropy of
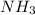
 = standard entropy of
= standard entropy of
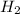
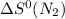 = standard entropy of
= standard entropy of
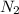
Now put all the given values in this expression, we get:
![\Delta S^o=[2mole* (192.5J/K.mole)]-[1mole* (191.5J/K.mole)+3mole* (130.6J/K.mole)]](https://img.qammunity.org/2020/formulas/chemistry/high-school/1uy79bsk6bas0bhvzohfzdby8xlavs8j0u.png)
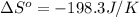
Therefore, the entropy change for the surroundings of the reaction is, -198.3 J/K