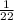Answer:
The height of the density function is
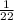
Explanation:
Given : A random variable X follows the continuous uniform distribution with a lower bound of −4 and an upper bound of 18.
To find : What is the height of the density function f(x)?
Solution :
According to question,
The height of the density function is given by,
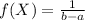
Where, a is the lower bound a=-4
b is the upper bound b=18
Substitute the value in the formula,
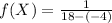

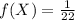
Therefore, The height of the density function is