Question

Which expression is equivalent to log3(x + 4)?

log3 - log(x + 4)
log12 + logx
log3 + log(x + 4)
log 3/log(x+4)

Answer 1

c

Explanation:

Answer 2

log[3(x+4)] is equal to log(3) + log(x + 4), which corresponds to choice number three.

Explanation:

By the logarithm product rule, for two nonzero numbers
`a` and
`b`,

`\log{(a \cdot b)} = \log{(a)} + \log{(b)}`.

Keep in mind that a logarithm can be split into two only if the logarithm contains the product or quotient of two numbers.

For example,
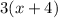`3(x + 4)` is the number in the logarithm
`\log{[3(x + 4)]}`. Since
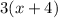`3(x + 4)` is a product of the two numbers
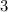`3` and
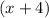`(x + 4)`, the logarithm
`\log{[3(x + 4)]}` can be split into two. By the logarithm product rule,

`\log{[3(x + 4)]} = \log{(3)} + \log{(x + 4)}`.

However,
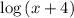`\log{(x + 4)}` cannot be split into two since the number inside of it is a sum rather than a product. Hence choice number three is the answer to this question.