Answer:
A)
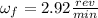 .
.
B)
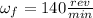 .
.
Step-by-step explanation:
A)
For this problem, we will use the conservation of angular momentum.
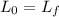 .
.
In the beginning, we have that
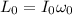
where
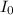 is the inertia moment of all the system at the starting position, this is the inertia moment of the rod plus the inertia moment of each ring (
is the inertia moment of all the system at the starting position, this is the inertia moment of the rod plus the inertia moment of each ring (
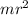 , with
, with
 the distance from the ring to the fixed axis and,
the distance from the ring to the fixed axis and,
 its mass) at the starting position and,
its mass) at the starting position and,
 is the initial angular velocity. So
is the initial angular velocity. So
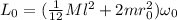 .
.
When the rings are at the ends of the rod the angular momentum becomes
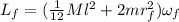 ,
,
where
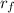 is the distance from the fixed axis to the end of the rod (the final position of the rings).
is the distance from the fixed axis to the end of the rod (the final position of the rings).
Using conservation of angular momentum we get
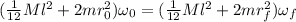 .
.
thus

computing this last expresion we get
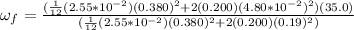
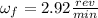 .
.
B)
Again we use the conservation of angular momentum. The initial angular momentum if the same as before. The final angular momentum will be
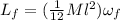 ,
,
this time we will not take into account the inertia moment of the rings because they are no longer part of the system (they leave the rod).
 .
.
thus
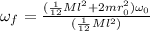
computing this last expresion we get
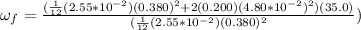
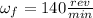 .
.