Question

Prove that if the set of vectors {u1, u2, u3} is linearly dependent and u4 is any vector, then the set {u1, u2, u3, u4} is linearly dependent.

Answer 1

Answer with Step-by-step explanation:

We are given that the set of vectors
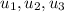`{u_1,u_2,u_3}` is lineraly dependent set .

We have to prove that the set
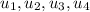`{u_1,u_2,u_3,u_4}` is linearly dependent .

Linearly dependent vectors : If the vectors
`u_1,u_2.u_3,u_4`

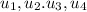
are linearly dependent therefore the linear combination

`a_1u_1+a_2u_2+a_3u_3+a_4u_4=0`

Then ,there exit a scalar which is not equal to zero .

Let
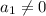`a_1\\eq0` then the vector
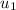`u_1` will be zero and remaining other vectors are not zero.

Proof:

When
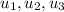`u_1,u_2,u_3` are linearly dependent vectors therefore, linear combination of vectors of given set

`a_1u_1+a_2u_2+a_3u_3=0`

By definition of linearly dependent vector

There exist a scalar which is not equal to zero.

Suppose
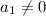`a_1\\eq 0` then
`u_1=0`

The linear combination of the set
`{u_1,u_2,u_3,u_4}`

`a_1u_1+a_2u_2+a_3u_3+a_4u_4=0`

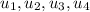
When
`a_1\\eq0\; and\; u_1=0`

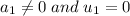
Therefore,the set
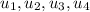`{u_1,u_2,u_3,u_4}` is linearly dependent because it contain a vector which is zero.

Hence, proved .