Answer:
Part 41) The solution of the compound inequality is equal to the interval [-1.5,-0.5)
Part 45) The solution of the compound inequality is equal to the interval
(-∞, -0.5] ∪ [1,∞)
Explanation:
Part 41) we have
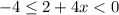
Divide the compound inequality into two inequalities
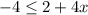 -----> inequality A
-----> inequality A
Solve for x
Subtract 2 both sides
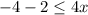
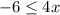
Divide by 4 both sides

Rewrite
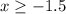
The solution of the inequality A is the interval -----> [-1.5,∞)
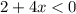 -----> inequality B
-----> inequality B
Solve for x
Subtract 2 both sides
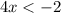
Divide by 4 both sides

The solution of the inequality B is the interval ------> (-∞, -0.5)
The solution of the inequality A and the Inequality B is equal to
[-1.5,∞)∩ (-∞, -0.5)------> [-1.5,-0.5)
see the attached figure N 1
Part 45) we have
 or
or
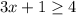
Solve the inequality A

Adds 3 both sides
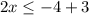
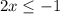
Divide by 2 both sides

The solution of the inequality A is the interval ------> (-∞, -0.5]
Solve the inequality B
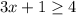
Subtract 1 both sides
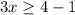
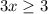
Divide by 3 both sides
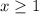
The solution of the inequality B is the interval -----> [1,∞)
The solution of the compound inequality is equal to
(-∞, -0.5] ∪ [1,∞)
see the attached figure N 2