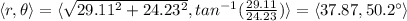Question

A football is kicked from the ground with a velocity of 38m/s at an angle of 40 degrees and eventually lands at the same height. What is the direction and magnitude of the ball's velocity 0.2 seconds after impact?

Answer 1

Initially, the velocity vector is
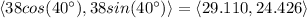`\langle 38cos(40^(\circ)),38sin(40^(\circ)) \rangle=\langle 29.110, 24.426 \rangle`. At the same height, the x-value of the vector will be the same, and the y-value will be opposite (assuming no air resistance). Assuming perfect reflection off the ground, the velocity vector is the same. After 0.2 seconds at 9.8 seconds, the y-value has decreased by
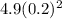`4.9(0.2)^2`, so the velocity is
`\langle 29.110, 24.426-0.196 \rangle = \langle 29.110, 24.23 \rangle`.

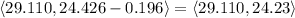Converting back to direction and magnitude, we get
`\langle r,\theta \rangle=\langle √(29.11^2+24.23^2),tan^(-1)((29.11)/(24.23)) \rangle = \langle 37.87,50.2^(\circ)\rangle`