Question

Noise levels at 5 airports were measured in decibels yielding the following data: 147,123,119,161,136 Construct the 99% confidence interval for the mean noise level at such locations. Assume the population is approximately normal. Calculate the sample standard deviation for the given sample data. Round your answer to one decimal place.

Answer 1

a) The 99% confidence interval for the mean noise level = [122.44, 151.96]

b) Sample standard deviation, s = 17.3dB

Step-by-step explanation:

Noise levels at 5 airports = 147,123,119,161,136

Mean noise level

`\bar{x} =( 147+123+119+161+136)/(5)=137.2dB`

Variance of noise level

`\sigma^2 =( (137.2-147)^2+(137.2-123)^2+(137.2-119)^2+(137.2-161)^2+(137.2-136)^2)/(5)\\\\\sigma^2=164.16`

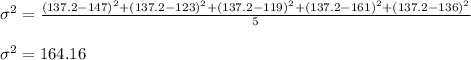
Standard deviation,

`\sigma =√(164.16)=12.81dB`

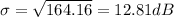
a) Confidence interval is given by

`\bar{x}-Z* (\sigma)/(√(n))\leq \mu\leq \bar{x}+Z* (\sigma)/(√(n))`

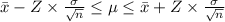
For 99% confidence interval Z = 2.576,

Number of noises, n = 5

Substituting

`137.2-2.576* (12.81)/(√(5))\leq \mu\leq 137.2+2.576* (12.81)/(√(5))\\\\122.44\leq \mu\leq 151.96`

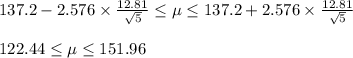
The 99% confidence interval for the mean noise level = [122.44, 151.96]

b) Sample standard deviation

`s=\sqrt{( (137.2-147)^2+(137.2-123)^2+(137.2-119)^2+(137.2-161)^2+(137.2-136)^2)/(5-1)}\\\\s=17.3dB`

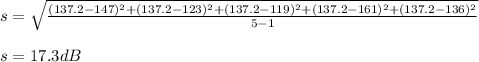
Sample standard deviation, s = 17.3dB