Answer:
height of prism =
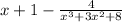
Explanation:
Volume of rectangular prism = (x^4+4x^3+3x^2+8x+4)
Area of its bases = (x^3+ 3x^2+8)
Height of prism = ?
Volume of rectangular Prism = Area of its bases * Height of prism
(x^4+4x^3+3x^2+8x+4) = (x^3+ 3x^2+8) * height of prism
=> height of prism = (x^4+4x^3+3x^2+8x+4) /(x^3+ 3x^2+8)
=> height of prism =
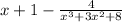
The division of (x^4+4x^3+3x^2+8x+4) /(x^3+ 3x^2+8) is shown in the attached figure.