Answer with explanation:
Given the function f from R to
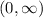
f:
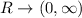
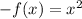
To prove that the function is objective from R to
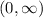
Proof:

When we prove the function is bijective then we proves that function is one-one and onto.
First we prove that function is one-one
Let
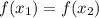
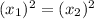
Cancel power on both side then we get
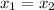
Hence, the function is one-one on domain [tex[(0,\infty)[/tex].
Now , we prove that function is onto function.
Let - f(x)=y
Then we get
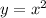

The value of y is taken from
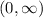
Therefore, we can find pre image for every value of y.
Hence, the function is onto function on domain
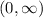
Therefore, the given
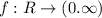 is bijective function on
is bijective function on
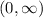 not on whole domain R .
not on whole domain R .
Hence, proved.