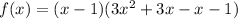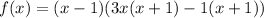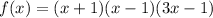Find the value of p for which the polynomial 3x^3 -x^2 + px +1 is exactly divisible by x-1, hence factorise the polynomial

Question

asked Oct 3, 2020 92.3k views

1 Answer

Jan Matousek · Answer 1 · 2020-10-08T16:31:37+0000

ANSWER

p = - 3

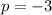
The completely factored form is

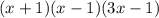
(x + 1)(x - 1)( 3x - 1)

Step-by-step explanation

The given polynomial expression is

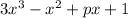
$3 {x}^(3) - {x}^(2) + px + 1$

Let

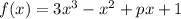
$f(x) = 3 {x}^(3) - {x}^(2) + px + 1$

According to the Remainder Theorem, if f(x) is exactly divisible by x-1, then the remainder is zero.

This implies that:

f(1) = 0

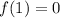
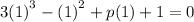
$3 {(1)}^(3) - {(1)}^(2) + p(1)+ 1 = 0$

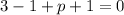
3 - 1 + p + 1 = 0

3 + p = 0

p = - 3

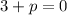
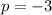
When we substitute the value of p back into the function, f(x) we get:

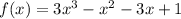
$f(x) = 3 {x}^(3) - {x}^(2) - 3x + 1$

We now perform long division as shown in the attachment.

We can factor the function to get:

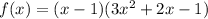
$f(x) =(x - 1)( 3 {x}^(2) + 2x - 1)$

We now split the middle term of the quadratic term and factor it completely to obtain:

$f(x) =(x - 1)( 3 {x}^(2) + 3x - x - 1)$

f(x) =(x - 1)( 3x(x + 1) - 1(x + 1))

f(x) =(x - 1)( 3x - 1)(x + 1)

f(x) =(x + 1)(x - 1)( 3x - 1)