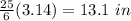Question

A circle has a radius of 5 in. A central angle that measures 150° cuts off an arc.

Explain how to find the arc length exactly, and then approximate it to one decimal place.​

Answer 1

13.1 (rounded to tenths)

Explanation:

150 ° into radian is 5/6.

150°/1 (π/180) =5π/6.

Then multiply the radian angle by the radius.

5π/6 (5) = 25π/6

25π/6 = 13.1 (rounded to tenths)

Answer 2

Part 1) The exact value of the arc length is
`(25)/(6)\pi \ in`

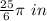
Part 2) The approximate value of the arc length is
`13.1\ in`

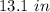
Explanation:

step 1

Find the circumference of the circle

The circumference of a circle is equal to

`C=2\pi r`

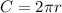
we have

`r=5\ in`

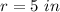
substitute

`C=2\pi (5)`

`C=10\pi\ in`

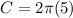
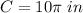
step 2

Find the exact value of the arc length by a central angle of 150 degrees

Remember that the circumference of a circle subtends a central angle of 360 degrees

by proportion

`(10\pi)/(360) =(x)/(150)\\ \\x=10\pi *150/360\\ \\x=(25)/(6)\pi \ in`

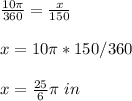
step 3

Find the approximate value of the arc length

To find the approximate value, assume

`\pi =3.14`

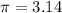
substitute

`(25)/(6)(3.14)=13.1\ in`