Question

A student answers a multiple-choice examination question that offers four possible answers. Suppose the probability that the student knows the answer to the question is 0.9 and the probability that the student will guess is 0.1. Assume that if the student guesses, the probability of selecting the correct answer is 0.25. If the student correctly answers a question, what is the probability that the student really knew the correct answer? (Round your answer to four decimal places.)

Answer 1

Answer: 0.9730

Explanation:

Let A be the event of the answer being correct and B be the event of the knew the answer.

Given:
`P(A)=0.9`

`P(A^c)=0.1`

`P(B|A^(C))=0.25`

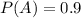
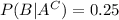
If it is given that the answer is correct , then the probability that he guess the answer
`P(B|A)= 1`

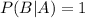
By Bayes theorem , we have

`P(A|B)=(P(B|A)P(A))/(P(B|A)P(A)+P(C|A^c)P(A^c))`

`=((1)(0.9))/((1))(0.9)+(0.25)(0.1))\\\\=0.972972972973\approx0.9730`

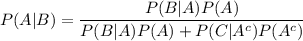
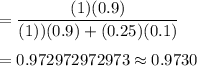
Hence, the student correctly answers a question, the probability that the student really knew the correct answer is 0.9730.