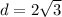Answer: Third option.
Explanation:
The distance between two points can be calculated with this formula:

Then, given the points
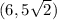 and
and
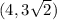 , we can identify that:
, we can identify that:
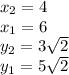
Now we must substitute these values into the formula:
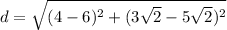
We get that the distance between these two points is: