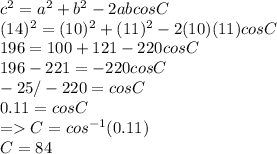Question

Determine whether angle ABC should be solved by using the Law of Sines or the Law of Cosines. Then solve the triangle.

a = 10, b = 11, c = 14

​

Answer 1

Law of Cosines; A ≈ 45.2°, B ≈ 51.3°, C ≈ 83.5°

Explanation:

Answer 2

Law of Cosines

Angle A = 45°

Angle B = 51°

Angle C = 84°

Explanation:

Law of sines is used when we are given

a) two angles and one side or

b) two sides and non-included angle

Law of cosines is used when we are given

a) three sides or

b) two sides and included angle

In the given question we are given three sides so, Law of Cosines will be used to solve the triangle.

Law of Cosines is:

`a^2 = b^2 + c^2 -2bccos A\\b^2 = a^2 + c^2 -2accos B\\c^2 = a^2 + b^2 -2abcosC`

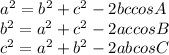
We will find the three angles A ,B and C of the triangle using above formula.

a= 10, b=11, c=14

Putting values and finding angle A

`a^2 = b^2 + c^2 -2bccos A\\(10)^2 = (11)^2 + (14)^2 -2(11)(14)cosA\\100 = 121 + 196 -308cosA\\100 = 317 -308 cosA\\100-317 = -308cosA\\-217/-308  = cos A\\0.704 = cos A\\=> A = cos ^(-1)(0.704)\\A= 45`

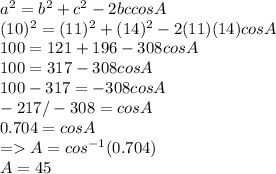
Now finding angle B

`b^2 = a^2 + c^2 -2ac cos B\\(11)^2 = (10)^2 + (14)^2 - 2(10)(14)cosB\\121 = 100+196 - 280cosB\\121 -296 = -280cosB\\-175/-280 = cosB\\0.625 = cosB\\=> B = cos^(-1) (0.625)\\B = 51`

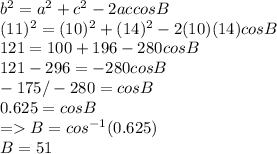
Now finding angle C

`c^2 = a^2 + b^2 -2abcosC\\(14)^2 =(10)^2 + (11)^2 -2(10)(11)cosC\\196 = 100+121 -220cosC\\196 -221 = -220cosC\\-25/-220 = cos C\\0.11 = cosC\\=> C = cos^(-1)(0.11)\\C= 84`