Can someone please help me? Use mathematical induction to prove the following. Please show your work. 13. (1)/(1(2)) +(1)/(2(3))+(1)/(3(4)) +...+(1)/(n(n+1)) =(n)/(n+1) Any help…

Question

asked May 17, 2020 230k views

2 Answers

Lizmary · Answer 1 · 2020-05-22T13:33:49+0000

First show it's true for
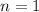n=1 . On the left,

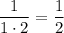
$\frac1{1\cdot2}=\frac12$

On the right,

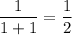
$\frac1{1+1}=\frac12$

so the base case
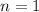n=1 is true.

Now assume equality holds for
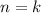n=k , that

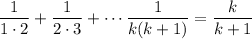
$\frac1{1\cdot2}+\frac1{2\cdot3}+\cdots\frac1{k(k+1)}=\frac k{k+1}$

We use this assumption to show it also holds for
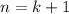n=k+1 . By hypothesis,

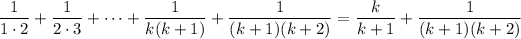
$\frac1{1\cdot2}+\frac1{2\cdot3}+\cdots+\frac1{k(k+1)}+\frac1{(k+1)(k+2)}=\frac k{k+1}+\frac1{(k+1)(k+2)}$

(the first
terms condense to
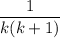$\frac1{k(k+1)}$ )

Combining the fractions gives

$(k(k+2))/((k+1)(k+2))+\frac1{(k+1)(k+2)}=(k^2+2k+1)/((k+1)(k+2))=((k+1)^2)/((k+1)(k+2))=(k+1)/(k+2)$

which is what we had to establish, thus proving (by induction) equality for all
.