Given that triangle PHT is a right triangle and Line HY is an altitude, what is the missing justification in the proof that (PH)^2 + (HT)^2 = (PT)^2?

Question

asked Oct 3, 2020 40.5k views

2 Answers

Dgzz · Answer 1 · 2020-10-05T14:32:56+0000

Answer:

The correct option is D.

Explanation:

Given information: Triangle PHT is a right triangle and Line HY is an altitude.

According to the reflexive property, a side or an angle is congruent to itself.

If A is an angle of a triangle then using reflexive property

$\angle A\cong \angle A$

$\angle PHT\cong \angle HYT$ (Both are right angles)

$\angle T\cong \angle T$ (Reflexive property)

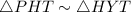$\triangle PHT\sim \triangle HYT$ (AA rule of similarity)

Other statements and reasons are present in the table.

The missing reason is reflexive property. Therefore the correct option is D.