What are the domain and range of the function f(x)=-square root x+3-2?

Question

asked Mar 12, 2020 76.7k views

2 Answers

Anit · Answer 1 · 2020-03-16T16:46:16+0000

For this case we have the following function:

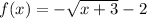
$f (x) = - \sqrt {x + 3} -2$

By definition, the domain is given by all the values for which the function is defined.

The given function is no longer defined if the argument of the root is negative. So:

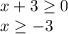
$x + 3 \geq0\\x \geq-3$

Thus, the domain of the function is given by all the values of x greater than or equal to -3.

Domain: [-3, ∞)

Substituting the values of the domain, we find the range.

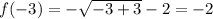
$f (-3) = - \sqrt {-3 + 3} -2 = -2$

The function evaluated in ∞ gives -∞. So the range is given by:

(-∞, 2]

Answer:

Domain: [-3, ∞)

Range: (-∞, 2]